Finite Element Analysis (FEA) can produce an enormous amount of data as output. Solution variables such as stress and strain are computed throughout an analysis for each increment and at each location within the model. These solution variables are computed at what are called “integration points”. These locations ARE NOT the same as the nodes of an element and it is important when post-processing FEA results to understand how the actual solution data is used to create contour plots, and how to extract accurate data representing the solution of the problem you are modeling. As is generally the case, it is the responsibility of the analyst to make sure the engineering is consistent with the problem at hand.
During a typical non-linear FEA solution process, numerous increments are taken to establish an equilibrated solution for the given applied loading. Stress equilibrium, strain compatibility and other mechanics equations are simultaneously “solved” by adjusting local solution variables such as stress and strain throughout the entire model being analyzed. These equations are written in such a way as to ultimately satisfy equilibrium conditions at an elemental level—the details of which depend on the shape function of the element being used. Regardless of element type and formulation, the shape functions determine how the discrete solutions for field variables like stress and strain are represented throughout an element, and compared with forces and displacements to evaluate the various equations governing the solution of the problem.
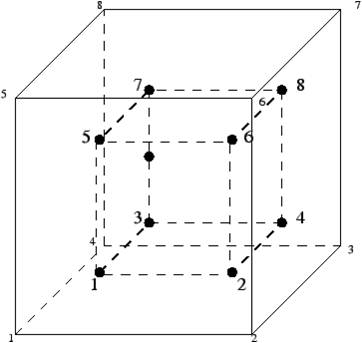
What is important to understand is that while forces and displacements are computed at nodal locations, stresses and strains are computed at integration points. The figure above for a typical 8-noded, linear, three-dimensional element illustrates the difference between nodal locations and integration points. The nodal locations are at the corners of the cube while the integration points are located within the element.
In order to generate contour plots from FEA results, it is necessary to extrapolate the stress or strain values from the integration points to the nodal locations. Since each node in a model will generally be shared by more than one element these extrapolated values will also have to be averaged in order to produce a smooth contour plot. While there are parameters that can be set to control how this process is handled by your post-processing software, there are many factors which can affect the accuracy of the extrapolated values.
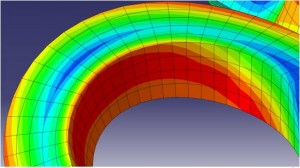
The degree to which the contour plot data differs from the actual data depends on the element type/formulation and particularly on the steepness of the underlying field variable gradient and to a large extent the quality of the underlying finite element mesh. Large gradients and a coarse mesh will obviously produce a greater degree of difference between the integration point data and extrapolated nodal averages.
Relying upon discrete data taken from contour plots for stress or strain can be misleading and inconsistent between various analysis runs. One reliable method for extracting specific stress and strain values is to use “integration point” data. In this way, you are assured of getting an accurate stress or strain value that relates directly to the solution of the underlying mechanics equations. However, in the case of performing a fatigue analysis, for example, stresses and strains at the surface of a component may be more relevant, as it is well known that cracks and defects generally initiate on the surface a part. In such a case, it is the analysts responsibility to understand the impact of using either integration point data or averaged nodal data.
The contour plot below on the left was produced with the nodal averaging turned off. You can see that when the nodal data is extrapolated for each element that the result produces discontinuities between adjacent elements. This is inevitable because the variation of stress and strain over an element is much more complicated than a simple linear relationship. The contour plot on the right was produced by turning nodal averaging back on. It is much smoother, but that smoothness comes with a loss of information.
[av_one_half first]
